Teil 1
| zur Übersicht |
| Zitatensammlung Teil 1 |
| Zitate von Rudolf STEINER zur |
| GEOMETRIE |
| 1a Und trotz alledem habe ich verhältnismäßig früh gut lesen gelernt. Dadurch konnte der Hilfslehrer mit etwas in mein Leben eingreifen, das für mich richtunggebend geworden ist. Bald nach meinem Eintreten in die Neudörfler Schule entdeckte ich in seinem Zimmer ein Geometriebuch. Ich stand so gut mit diesem Lehrer, daß ich das Buch ohne weiteres eine Weile zu meiner Benutzung haben konnte. Mit Enthusiasmus machte ich mich darüber her. Wochenlang war meine Seele ganz erfüllt von der Kongruenz, der Ähnlichkeit von Dreiecken, Vierecken, Vielecken; ich zergrübelte mein Denken mit der Frage, wo sich eigentlich die Parallelen schneiden; der pythagoreische Lehrsatz bezauberte mich. |
| 1b Daß man seelisch in der Ausbildung rein innerlich angeschauter Formen leben könne, ohne Eindrücke der äußeren Sinne, das gereichte mir zur höchsten Befriedigung. Ich fand darin Trost für die Stimmung, die sich mir durch die unbeantworteten Fragen ergeben hatte. Rein im Geiste etwas erfassen zu können, das brachte mir ein inneres Glück. Ich weiß, daß ich an der Geometrie das Glück zuerst kennen gelernt habe. |
| aus «Mein Lebensgang»; S.20f |
| nach oben |
| 2a Die Alten haben in ihrem Wissen immer eine Verwandtschaft gefühlt zwischen dem Nervenmark, der Nervensubstanz und dem Knochenmark oder der Knochensubstanz, und sie sind der Meinung gewesen, daß man mit dem Knochenteil ebenso denkt wie mit dem Nerventeil. Das ist auch die Wahrheit. Wir verdanken alles, was wir an abstrakter Wissenschaft haben, der Fähigkeit unseres Knochensystems. Warum kann der Mensch zum Beispiel Geometrie ausbilden? Die höheren Tiere haben keine Geometrie; das sieht man ihrer Lebensweise an. Es ist nur ein Unsinn, wenn manche Leute sagen: Vielleicht haben die höheren Tiere auch Geometrie, man merkt es vielleicht nur nicht. - Der Mensch also bildet Geometrie aus. Wodurch aber bildet er zum Beispiel die Vorstellung eines Dreiecks aus? Wer wirklich über diese Tatsache nachdenkt, daß der Mensch die Vorstellung des Dreiecks ausbildet, der muß etwas Wunderbares darin finden, daß der Mensch das Dreieck, das abstrakte Dreieck, das im konkreten Leben nirgends vorhanden ist, rein aus seiner geometrisch-mathematischen Phantasie heraus ausbildet. Es liegt vieles Unbekannte zugrunde den Geschehnissen der Welt, die offenbar sind. Denken Sie sich zum Beispiel an einem bestimmten Platze dieses Zimmers stehend. Sie führen zu gewissen Zeiten als übersinnliches Menschenwesen merkwürdige Bewegungen aus, von denen Sie für gewöhnlich nichts wissen, ungefähr in der Art: Sie gehen ein Stückchen nach der einen Seite, dann gehen Sie ein Stückchen zurück, und dann kommen Sie wieder an Ihrem Platze an. Eine unbewußt bleibende Linie im Raume, die Sie beschreiben, verläuft tatsächlich als eine Dreiecksbewegung. Solche Bewegungen sind tatsächlich vorhanden, Sie nehmen sie nur nicht wahr, aber dadurch, daß Ihr Rückgrat in die Vertikale gerückt ist, sind Sie in der Ebene drinnen, in der diese Bewegungen verlaufen. Das Tier ist nicht in dieser Ebene drinnen, es hat sein Rückenmark anders liegen; da werden diese Bewegungen nicht vollführt. Indem der Mensch sein Rückenmark vertikal stehen hat, ist er in der Ebene, wo diese Bewegung ausgeführt wird. Zum Bewußtsein bringt er es sich nicht, daß er sich sagte: Ich tanze da fortwährend in einem Dreieck. - Aber er zeichnet ein Dreieck und sagt: Das ist ein Dreieck! - In Wahrheit ist das eine unbewußt ausgeführte Bewegung, die er im Kosmos vollführt. |
| 2b Diese Bewegungen, die Sie in der Geometrie fixieren, indem Sie geometrische Figuren zeichnen, führen Sie mit der Erde aus. Die Erde hat nicht nur die Bewegung, welche sie nach der Kopernikanischen Weltansicht hat: sie hat noch ganz andere, künstlerische Bewegungen, die werden da fortwährend ausgeführt. Und noch viel kompliziertere Bewegungen werden ausgeführt, solche Bewegungen zum Beispiel, die in den Linien liegen, welche die geometrischen Körper haben: der Würfel, das Oktaeder, das Dodekaeder, das Ikosaeder und so weiter. Diese Körper sind nicht erfunden, sie sind Wirklichkeit, nur unbewußte Wirklichkeit. Es liegen in diesen und in noch anderen Körperformen merkwürdige Anklänge an dieses für die Menschen unterbewußte Wissen. Das wird dadurch herbeigeführt, daß unser Knochensystem eine wesentliche Erkenntnis hat; aber Sie reichen nicht mit Ihrem Bewußtsein bis zum Knochensystem hinunter. Das Bewußtsein davon erstirbt, es wird nur reflektiert in den Bildern der Geometrie, die der Mensch da als Bilder ausführt. Der Mensch ist recht sehr eingeschaltet in den Kosmos. Indem er die Geometrie ausbildet, bildet er etwas nach, was er selbst im Kosmos tut. |
| Stuttgart, 23.Aug.1919 ♄ (aus «GA 293»; S.56ff) |
| nach oben |
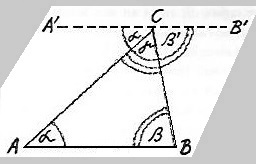
| 3a Nun, von der Ecke, von der zuerst etwas wie ein Zwang zum Beweglichmachen des arithmetischen und des geometrischen Denkens gekommen ist, möchte ich Ihnen zuerst sprechen. Nicht wahr, die Geometrie war etwas sehr altes. Wie man sich aus der Geometrie heraus Gesetzmäßigkeiten an Linien, Dreiecken, Vierecken usw. vorstellt, das ist etwas Althergekommenes und das hat man angewendet auf dasjenige, was sich einem als äußere Erscheinungen in der Natur bietet. Nun ist aber gerade vor dem Denken des neunzehnten Jahrhunderts diese Geometrie etwas ins Wanken gekommen, und das ist auf die folgende Weise geschehen: Nicht wahr, versetzen Sie sich wiederum gut auf die Schulbank, so wissen Sie, überall wird Ihnen gelehrt - und unsere lieben Waldorfschullehrer lehren es selbstverständlich auch, müssen es ja lehren -, wenn man ein Dreieck hat und die drei Winkel nimmt, so sind diese drei Winkel zusammen ein gestreckter oder 180°. Das ist Ihnen bekannt. Nun fühlt man sich natürlich gedrängt - und muß sich gedrängt fühlen -, auch den Schülern eine Art Beweis zu geben dafür, daß diese drei Winkel zusammen 180° sind. Man macht ja das dadurch, daß man hier eine Parallele zieht zu der Grundlinie des Dreiecks, daß man sagt: Derselbe Winkel, der hier als a ist, zeigt sich hier als α', α und α' sind Wechselwinkel. Sie sind gleich. Ich kann also einfach diesen Winkel hier herüberlegen. |
 |
| Ebenso kann ich diesen Winkel β hier herüberlegen und habe hier das gleiche. Nun, der Winkel γ bleibt ja liegen, und wenn γ = γ und α' = α und β' = β ist und α'+β'+γ zusammen einen gestreckten Winkel geben, so müssen auch α+β+γ einen gestreckten Winkel zusammen bilden. Ich kann also das klar anschaulich beweisen. Etwas Klareres und Anschaulicheres kann es, möchte man sagen, gar nicht geben. |
| 3b Nun aber, die Voraussetzung, die man da macht, indem man dies beweist, ist die, daß diese obere Linie A'-B' parallel ist zu A-B. Denn nur dadurch bin ich in der Lage, den Beweis zu führen. Nun gibt es aber in der ganzen Euklidschen Geometrie kein Mittel zu beweisen, daß zwei Linien parallel sind, das heißt sich in unendlicher Entfernung erst schneiden, das heißt gar nicht schneiden. Das sieht so aus, als ob sie parallel wären, nur solange ich beim gedachten Raum bleibe. Nichts verbürgt mir, daß das auch bei einem wirklichen Raum so der Fall ist. Und wenn ich daher nur das eine annehme, daß diese beiden Geraden sich nicht in unendlicher Entfernung erst schneiden, sondern sich real früher schneiden, dann geht mein ganzer Beweis für die 180° der Dreieckswinkel kaputt, dann würde ich herausbekommen, daß zwar nicht in dem Raum, den ich mir selber in Gedanken konstruiere und mit dem sich die gewöhnliche Geometrie befaßt - in diesem Raum haben die Dreieckswinkel 180° als Winkelsumme -, daß aber, sobald ich einen vielleicht anderen, wirklichen Raum ins Auge fasse, die Winkelsumme des Dreiecks gar nicht mehr 180°, sondern vielleicht größer ist. Das heißt, es sind außer der gewöhnlichen, von Euklid herstammenden Geometrie noch andere Geometrien möglich, für welche die Summe der Dreieckswinkel durchaus nicht 180° ist. Mit Auseinandersetzungen nach dieser Richtung hat sich das Denken des neunzehnten Jahrhunderts, namentlich seit Lobatschewskij, viel beschäftigt, und daran anschließend mußte doch die Frage entstehen: Sind denn nun eigentlich die Vorgänge der Wirklichkeit, die wir da verfolgen mit unseren Sinnen, wirklich auch zu fassen, vollgültig zu fassen mit denjenigen Vorstellungen, die wir als geometrische Vorstellungen in dem von uns gedachten Raum gewinnen? Der von uns gedachte Raum ist zweifellos gedacht. Wir können zwar als eine schöne Vorstellung hegen, daß dasjenige, was da draußen außer uns geschieht, teilweise zusammentrifft mit demjenigen, was wir darüber aushecken, aber es garantiert uns nichts dafür, daß dasjenige, was draußen geschieht, so wirke, daß wir es restlos begreifen durch die von uns ausgedachte Euklidsche Geometrie. Es könnte sehr leicht sein - darüber könnten uns aber nur die Tatsachen selber belehren -, daß die Dinge draußen nach einer ganz anderen Geometrie vorgehen und wir sie erst bei unserer Auffassung übersetzen in die Euklidsche Geometrie und ihre Formeln. Das heißt, wir haben zunächst, wenn wir uns bloß einlassen auf dasjenige, was der Wissenschaft der Natur heute zur Verfügung steht, gar keine Möglichkeit, irgend etwas zunächst darüber zu entscheiden, wie sich verhalten unsere geometrischen, überhaupt die phoronomischen Vorstellungen zu demjenigen, was uns draußen in der Natur erscheint. Wir rechnen, zeichnen die Naturerscheinungen, insoferne sie physikalisch sind. Aber ob wir da irgend etwas nur äußerlich an der Oberfläche zeichnen oder in irgend etwas von der Natur eindringen, darüber ist zunächst ja nichts auszumachen. Und wenn man einmal anfangen wird, gründlichst zu denken in der namentlich physikalischen Naturwissenschaft, dann wird man in eine furchtbare Sackgasse hineinkommen, dann wird man sehen, wie man nicht weiterkommt. Und man wird nur weiterkommen, wenn man sich zuerst belehren wird über den Ursprung unserer phoronomischen Vorstellungen, unserer Vorstellungen über das Zählen, über das Geometrische und auch unserer Vorstellungen über die bloße Bewegung, nicht über die Kräfte. |
| 3c Woher kommen denn alle diese phoronomischen Vorstellungen? Man kann so gewöhnlich den Glauben haben, sie kommen aus demselben Grunde heraus, aus dem die Vorstellungen kommen, die wir auch gewinnen, wenn wir uns auf die äußeren Tatsachen der Natur einlassen und diese verstandesmäßig bearbeiten. Wir sehen durch unsere Augen, hören durch unsere Ohren, wir verarbeiten das durch die Sinne Wahrgenommene mit dem Verstande zunächst primitiv, ohne daß wir es zählen, ohne daß wir es zeichnen, ohne daß wir auf die Bewegung schauen. Wir richten uns nach ganz anderen Begriffskategorien. Da ist unser Verstand an der Hand der Sinneserscheinungen tätig. Aber wenn wir nun anfangen, sogenannt wissenschaftliche Geometrie-, Arithmetik-, Algebra- oder Bewegungs-Vorstellungen anzuwenden auf dasjenige, was da äußerlich vorgeht, dann tun wir doch etwas anderes noch, dann wenden wir Vorstellungen an, die wir ganz sicher nicht aus der Außenwelt gewonnen haben, sondern die wir aus unserem Inneren herausgesponnen haben. Woher kommen denn diese Vorstellungen eigentlich? - das ist die Kardinalfrage. Diese Vorstellungen, die kommen nämlich gar nicht aus unserer Intelligenz, die wir anwenden, wenn wir die Sinnesvorstellungen verarbeiten, sondern diese Vorstellungen kommen eigentlich aus dem intelligenten Teile unseres Willens, die machen wir mit unserer Willensstruktur, mit dem Willensteil unserer Seele. Es ist ein gewaltiger Unterschied zwischen allen anderen Vorstellungen unserer Intelligenz und den geometrischen, arithmetischen und Bewegungs-Vorstellungen. Die anderen Vorstellungen gewinnen wir an den Erfahrungen der Außenwelt; diese Vorstellungen, die geometrischen, die arithmetischen Vorstellungen, die steigen auf aus dem unbewußten Teile von uns, aus dem Willensteile, der sein äußeres Organ im Stoffwechsel hat. Daraus steigen zum Beispiel im eminentesten Sinne die geometrischen Vorstellungen auf. Sie kommen aus dem Unbewußten im Menschen. Und wenn Sie anwenden diese geometrischen Vorstellungen - ich werde sie jetzt gebrauchen auch für die arithmetischen und algebraischen Vorstellungen -, wenn Sie sie anwenden auf Lichterscheinungen oder Schall- oder Tonerscheinungen, dann verbinden Sie in Ihrem Erkenntnisprozeß dasjenige, was Ihnen von innen aufsteigt, mit demjenigen, was Sie äußerlich wahrnehmen. Unbewußt bleibt Ihnen dabei der ganze Ursprung der aufgewendeten Geometrie. Sie vereinigen diese aufgewendete Geometrie mit den äußeren Erscheinungen; unbewußt bleibt Ihnen der ganze Ursprung. |
| Stuttgart, 3.Jän.1920 ♄ (aus «GA 320»; S.167ff) |
| nach oben oder zur Übersicht |
| revid.201808 |
| https://wfgw.diemorgengab.at/zit/WfGWzit102800020.htm |